When it comes to random number generation on computers that do not feature dedicated hardware random number generators, the only solution is to operate a pseudo random number generator (PRNG). In this context, one faces the problem of providing high entropy seed data to initialize the PRNG if it shall be used in cryptographic operations. On general purpose computers, various sources for entropy are sampled by the operating system random number generators (RNGs), such as I/O timings, mouse movements and timings of key strokes. However, on embedded systems, often all of these sources are unavailable. In this case, a proposed approach is to use the content of the uninitialized RAM at system start-up as an entropy source. Furthermore, even OpenSSL, not specifically designed for embedded systems, in its RNG implementation uses the previous content of buffers to be overwritten with random bytes as additional seed data for the random number generation. Generally, such a buffer must be assumed to contain uninitialized data. This detail has received great attention in the context of the Debian random number generation fiasco, when a Debian developer removed function calls reported by memory checking tools to access uninitialized data. However, it turned out that these calls where actually necessary and their removal drastically reduced the entropy level of the RNG.

Given these connections between uninitialized data and random number generation, I want to call attention to a problem that arises from the treatment of uninitialized data by C compilers. We will find that the usage of uninitialized data in computations incurs the risk that the resulting code may have completely different properties than intended and that there are far greater risks than the contribution of the uninitialized data to the RNG's entropy level being low or zero.

We will begin the analysis of this problem with a real-world example described by Xi Wang. This is probably the first report that brings this problem domain to attention. However, Wang gives a rather brief analysis, and here we are going to look at the potential consequences in a wider scope. The example is about the following code snippet:

struct timeval tv;
unsigned long junk;

gettimeofday(&tv, NULL);
srandom((getpid() << 16) ^ tv.tv_sec ^ tv.tv_usec ^ junk);

The variable junk is used as an uninitialized 32-bit value to provide another source of entropy additional to the PID and time value. Up to a certain compiler version the resulting program code performed the computation as intended. However, the newer comiler version suddenly did only the following: it called gettimeofday and getpid, both times ignoring the return value, and then called srandom with an uninitialized value. (For the details concerning the affected program and involved compiler, please refer to the above link.)

To most of us it is probably a surprise that the generated code is conforming to the C standard. In the C99 standard, the central statement about uninitialized variables (or buffers) is "If an object that has automatic storage duration is not initialized explicitly, its value is indeterminate". Intuitively, I claim, this leads us to the following assumption about the treatment of the uninitialized variable junk by the compiler: it reserves some register or space on the stack for this variable. Whatever value is in that register or in that area of the stack, effectively becomes the initialization value of that variable. This is exactly how the code generated by the older compiler versions behaved (it used the value found in register ebx). We will soon see that this view cannot explain what happened with the newer compiler version, but it is possible to demonstrate that already under this assumed compiler behaviour problems can result, as we demonstrate in our "zeroth" explanation. Afterwards, we will give two other explanations that actually apply to Wang's example.

The compiler is entirely free to choose the order of the computations in line 5 and the allocation of the variable junk. Thus it might first carry out the first two XOR computations. It might then allocate junk with the effective initial value of tv.tv_sec ^ tv.tv_usec as an intermediate result of the previous computation left over in a register or on the stack. Thus, being XOR-added twice, the contribution of the time value is cancelled. We learn from this that "indeterminate value" can also mean that the value of an uninitialized variable is closely related to other variables' values in the program execution.

However, this is not what happened in Wang's example, since otherwise srandom could not have been called with a completely uninitialized value. (If for some reason junk had the value of the result of the other two XOR operations, then srandom would have to be called with the value zero.) To understand how the compiler came to the generation of this code, we have to give up our intuitive assumption that it has to allocate the uninitialized variable somewhere, in a register or memory, and thus explicitly assign it a value.

Let us label the argument to srandom as A, i.e. A = (getpid() << 16) ^ tv.tv_sec ^ tv.tv_usec ^ junk. Analysing the code of line 5, the compiler finds that junk completely controls A in the following sense: for each value of the result of the other two XOR computations not involving junk, and any possible value of A, there exists a corresponding value of junk. This means that just any value can be passed to srandom. The point of view of the compiler can be summarized as follows: "junk is indeterminate. The implementer chose to put up with any result of the overall computation that could be reached by any possible initial value of junk. I do not have to carry out the computation of A, as for any possible value of A I can claim to have implicitly chosen a value of junk." Indeed, every execution of the program will be valid in this sense. Our expectation that the statistical properties of the argument passed to srandom will be as intended, is based on the implicit and erroneous assumption that an indeterminate value will be chosen unrelated to other values in the program.

Another explanation for the generation of the vulnerable code is that the compiler realised what is referred to by the C standard as "undefined behaviour". The clause that allows this is that access to uninitialized data other than as an unsigned char may have a trap representation. Since junk is of a different type, this issue may apply here. The effect of a trap value can lead to control flows and thus computation results that are impossible for any valid initial value of a variable, as an example with an uninitialized boolean value shows.

From these considerations we understand that in Wang's example, the compiler behaves correctly, either by Explanation 1 or 2. Now we explore what this result means for the employment of uninitialized data for random number generation in general.

First, we turn to approaches that are clearly at risk of suffering from this freedom of the compiler. Assume, for instance, that an implementer chooses to use the start-up values of the RAM of an embedded system as a source of entropy. Due to performance considerations, instead of using a hash function directly, he partitions the RAM into a number of equally sized segments and computes the sum of the 32-bit words contained in each of these segments separately. Afterwards, he computes a hash value over the concatenation of these sums. Though this approach is not optimal from a cryptographic perspective, it can be assumed to produce a reasonably secure seed value (under the assumption that the RAM values contained sufficient entropy), especially if a large number of segments is used. However, due to the compiler's freedom concerning uninitialized memory, a C implementation of this algorithm is at risk to produce low or even zero entropy seeds: not a single sum computation might be carried out, all the 32-bit words fed to the hash function might end up having the same value.

Now we consider the security of OpenSSL's feature of employing uninitialized data in the random number generation. OpenSSL's random number generator is implemented in the file md_rand.c. Providing a description of this RNG would be beyond of the scope of this analysis, however, we are only interested in the processing of the potentially uninitialized data in the buffer to be filled with random bytes, referred to as the target buffer in the following, during the random number generation. OpenSSL's RNG computes the random output in the function ssleay_rand_bytes() by feeding different parts of its internal state as well as the contents of the target buffer into a SHA1 computation. In order for the compiler to be able to apply the reasoning as described in Explanation 1 and thus to remove or alter the call to the SHA1 computation, it would have to be able to reason that for any possible resulting SHA1 state, there exists a value of the target buffer that causes this resulting state. This would imply the inversion of SHA1, which certainly is beyond the compiler's possibilities. We could consider whether the approach provided in Example 2 is applicable. Taking a look at the SHA1 implementation in OpenSSL, we find that the input data is read as unsigned char, and thus the compiler cannot resort to undefined behaviour. From this perspective, there is no reason to worry about OpenSSL's usage of the initial values of the target buffer.

Contrasting the apparent safety of OpenSSL's processing of uninitialized memory, we can indeed construct a potentially vulnerable example of a hash function implementation. To elaborate this, let us consider a cipher-based hash function such as the Matyas–Meyer–Oseas construction. The compression function of the Matyas–Meyer–Oseas hash construction is shown in the following figure.

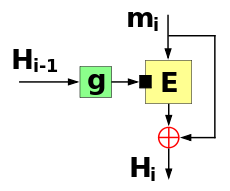
Here Hi-1 denotes the previous hash state, mi denotes the current message block and Hi is the updated hash state. The previous hash state is preprocessed by some function g, the output of which is set as the cipher key. Then the new message block is encrypted, and the ciphertext block XORed by the message block is the updated value of the hash state.

Now we ask the following question: if mi is uninitialized data, is the compiler allowed (based on the considerations given in Explanation 1) to reason that mi completely controls the resulting state Hi-1, and thus set the resulting state Hi to some arbitrary value that is independent of Hi-1? Based on our previous considerations on the compiler's freedom, we must answer this question by "no": The value of mi also enters the cipher operation, thus the compiler cannot take on the view to have implicitly chosen a value for mi in order to set Hi to an arbitrary value. We still expect the compiler to produce only programs that behave in such way that there is an implicit choice of the value of the uninitialized data. In order to alter the code in the way described above, the compiler would have to suppose two different values for mi at two different points in the program. Based on indeterminate values that are not trap representations, this seems forbidden by the C standard.

But let us now assume that the XOR operation in the Matyas-Meyer-Oseas compression function is implemented 32 bit word wise. In this case, the compiler could, if our analysis in Explanation 2 is correct, indeed assume a different value for mi at different points in the program, as this would be covered by undefined behaviour. Accordingly, the entire call to the compression function could be at risk of being removed.

An actual trap value, i.e. an invalid data representation for the CPU, might not even be realized in on a given platform. From my understanding of the C standard, the clause about uninitialized data that is accessed other than as an unsigned char generally gives the compiler the freedom to implement undefined behaviour.

Another way to accumulate the entropy of uninitialized memory would be to compute the CBC-MAC of the memory contents, which amounts to computing the final CBC ciphertext of the CBC encryption of the data. The initialization vector can be chosen as a zero string and the key may be hard-coded in the program. In the CBC mode, each ciphertext block is computed as C_i = E_k(C_i-1 ⊕ P_i), where E_k() is the cipher encryption under the key k, C_i-1 is the previous ciphertext block and P_i is the current plaintext block. If P_i is uninitialized, we must fear that the compiler can apply the reasoning described in Explanation 1 and thus make the XOR result independent of both C_i-1 and P_i, completely subverting the intended entropy accumulation.

Comparing the CBC case or any of the theoretically discussed examples with Wang's example, we realise that in contrast to the latter they all share the property that the uninitialized data is not allocated in the same function as where it is used in the computation. That indeed calls for greater optimization capabilities in the compiler in order to be able to produce vulnerable code. However, the employment of optimization capabilities that work across function call boundaries was already demonstrated by the issue where a compiler removed a call to memset() because it realized that the overwritten data was not used any more before their validity ended. That call was intended to clear sensitive data, which might otherwise reappear in uninitialized buffers subsequently during program execution.

Optimizations such as those that lead to the memset() issue and those that would be necessary to create vulnerable code in the face of uninitialized data fed to a CBC function imply that they are able to cross function boundaries. At least if the functions are in separate compilation units, such optimizations must generally be carried out in the link stage rather than in the compilation stage. However, at this stage, it will still be possible for the compiler to determine that a certain variable is not initialized, and thus it is not obvious that critical optimizations in the context of the processing of uninitialized data are any more challenging to a compiler than those that lead to the memset() issue.

However, what might aggravate the situation for the compiler is if his reasoning does not simply lead to the removal of a function call as it is the case in the memset() issue, but only for the execution of a simplified version of that function. It is rather unlikely that, as a consequence, the compiler will generate different versions of the same function, though this is certainly allowed by the C standard. On the other hand, the compiler might choose to simply inline the necessary remaining code at the call site. In the case of CBC, this might be simply a call to the cipher encryption function, which might not even increase the code size at the modified call site.

Note that there is also a construction that would allow for the complete removal of the call: that is encryption in the CFB mode. From a theoretic perspective, the CFB mode would also be a suitable solution for entropy accumulation. There, the very last operation is the XOR of the plaintext (assumed to be uninitialized) to a cipher output, the result of which thus is arbitrary from the critically-optimizing compiler's point of view.

This leads us to the question of countermeasures. Assembler implementations of the entropy accumulation function will probably not solve the problem, since an optimizer might affect them equally as C code (note that also memset() is typically implemented in assembler). For the indispensable entropy accumulation at system start-up, the only solutions seem to be manual or automated verification of the produced binary code. In places where the usage of uninitialized data is not essential, it might make sense to avoid it completely. Otherwise, algorithms should be designed so that the effect of compiler optimizations is at least restricted. That means that if uninitialized data is used in a hash computation together with other data, it should be fed to the hash function first. In this way, the compiler might assign an arbitrary value to the hash state after that operation (e.g. leave it untouched, except for a potential update of the length counter in the state), but it has no reason to alter or remove subsequent calls that feed further data (such as OpenSSL's RNG feeds parts of the hash state).

Furthermore, concerning the choice of the function for entropy accumulation, a standard hash function such as MD5 (the weaknesses of which are of no relevance for this purpose), SHA1, or one from the SHA2 family should be favored over any cipher-based construction. This is due to the complicated processing of the input data in standard hash functions, which we must assume to aggravate the possibilities of dangerous compiler optimizations considerably, compared to the extreme case of the exposed XOR operations involving potentially uninitialized data in the cipher-based constructions.

The use of the volatile specifier is often suggested to prevent compiler optimizations, for instance in the context of the memset() issue. In general it might be a valid countermeasure to let the hash function access the input data as a volatile variable. However, there are results by Eide and Regehr showing that implementations of volatile in compilers are often faulty.

From Wang's example we already learn that the usage of uninitialized data in C programs can lead to the subversion of entropy accumulation. We provided an analysis that suggests two possible explanations for the legitimacy of the removal of the computation involving an uninitialized variable. Explanation 1 argues that the compiler is not bound to produce a program that explicitly commits itself to a value of an uninitialized variable prior to using it in computations, but rather may arrange the code such that there always exists a specific value of the uninitialized variable that would have led to the computation result. This behaviour is possible with any type of variable. In Explanation 2, we make use of the fact that the C standard allows for undefined behaviour in the processing of uninitialized data of a type other than unsigned char. This, in my understanding, gives the compiler much greater freedom concerning the resulting code, including the possibility to imply different values for the same uninitialized variable at different points in the program. As a result, a far greater range of optimizations are feasible. For the example of cipher-based hash functions or certain block cipher modes, we have shown that even such functions calls, if they process uninitialized data, are at risk to altered or removed by an optimizer. A comparison with the issue of optimization-resistant secret wiping showed us that the necessary optimization approaches of compilers might already allow for cross-function-boundary optimizations that are necessary to produce vulnerable code.

• A collection of examples of interesting compiler behaviour
• A CERT article that mentions Wang's example but describes the consequences of the compiler behaviour incorrectly
• Some more information on trap representations